El oculto legado matemático de los mayas
- Details
- Mundo / América Latina|
- 26 Febrero 2024|
- Diego Daniel García|
- 1825 x
Yury Valentinovich Knorozov (nacido el 19 de noviembre de 1922 en Jarkov, U.R.S.S.; fallecido el 31 de marzo de 1999 en Moscú, Rusia) fue un lingüista, epigrafista y etnólogo ruso que desempeñó un papel importante en el desciframiento de la escritura jeroglífica maya.
Knorozov aportó un nuevo enfoque innovador a este campo en un artículo publicado en la revista “Etnografía soviética” en 1952. En él argumentó que los glifos escritos por los antiguos indios mayas constan de logogramas (signos utilizados para representar una palabra entera) o de signos fonéticos; en el caso de este último, cada glifo representa una combinación consonante-vocal.

Knorozov continuó postulando correctamente que una palabra maya formada por una combinación consonante-vocal-consonante estaba escrita con dos glifos, y la vocal del segundo glifo no se pronunciaba.
Publicó su principal libro sobre el tema, “La escritura de los indios mayas”, en 1963. Su hipótesis fonética obtuvo una amplia aceptación en la década de 1970 y permitió leer en su totalidad muchas inscripciones mayas antiguas. Entre las numerosas obras que pudieron ser decifradas gracias al trabajo de Knorozov, se encuentra el famoso “códice de Dresde”.
El Códice de Dresde es un libro maya, que data del siglo XI o XII. El códice fue redescubierto en la ciudad de Dresde, Alemania, de ahí el nombre actual del libro. En el presente, este antiguo manuscrito está ubicado en el museo de la Biblioteca Estatal de Sajonia. El códice contiene información relativa a tablas astronómicas y astrológicas, referencias religiosas, estaciones de la tierra y enfermedades y medicinas.
También incluye información sobre conjunciones de planetas y lunas. El libro sufrió daños por agua durante la Segunda Guerra Mundial, pero a pesar de ello, el material sobrevivió a pesar de que sus páginas están hechas de amate y tienen 20 cm de alto. Estas páginas se pueden doblar en forma de acordeón; cuando está desplegado, el códice mide 3,7 m (12 pies) de largo. Está escrito en jeroglíficos mayas y hace referencia a un texto original de unos trescientos o cuatrocientos años antes, que describe la historia local y tablas astronómicas.
Imágenes: Knorozov junto a su gato siamés.

Los mayas poseían varios calendarios que reflejaban sus profundos conocimientos matemáticos, astronómicos, y hasta de biología. El calendario maya más sagrado y antiguo se llamaba tzol'kin, un calendario de 260 días compuesto por una doble cuenta de 20 ciclos de 13 días cada uno, y 13 ciclos de 20 días, ya que aparentemente, los números 13 y 20 eran usados por los mayas en una forma similar en la que hoy día se usa el 0 y el 1 para conformar el código binario moderno. Se postula que 263 días es el tiempo que demora Venus en aparecer y desaparecer en el horizonte en su subida y caída como astro que aparece en las mañanas y en las tardes. Si a estos 263 días les descontamos los equinoccios, nos da 260 días. La cuenta larga maya utilizaba un ciclo de 20 días llamado uinal, uno de 360 días llamado tun, uno de 7.200 llamado katún, y uno de 144.000 días llamado baktún. La cuenta larga es 13 periodos de 144.000 días, o sea 13 baktunes, que equivale a 1.872.000 kines (días), que a su vez equivale a 7.200 ciclos tzol’kin o 5.200 tunes, o a 20 ciclos ahau de 93.600 días. Un ahau es a su vez 360 tzol'kin. Las cifras en kines que expresan los ciclos tienen la particularidad de reducirse a 9: 360 (3+6 = 9), 7.200 (7+2 = 9), 144.000 (1+4+4 = 9), 1.872.000 (1+8+7+2 = 18; 1+8 = 9), 93.600 (9+3+6= 18; 1+8 = 9). Lo mismo ocurre con los ciclos mas largos no usados de forma tan frecuente por los mayas: piktún, kalabtún, kinchinltún, y alautún. Veinte baktunes formarían un piktún de aproximadamente 7.890 años y veinte piktunes generan un kalabtún de 57.600.000 kines, aproximadamente 157.810 años, y vemos que 5+7+6= 18; 1+8= 9. El número del albedo de Venus, 65, multiplicado por 4 nos da la cantidad de días del tzol'kin, y como ha sido observado, si sumamos los números de las cuatro esquinas que podemos observar en el sincronario tzol'kin (1, 7, 7, 13), encontraremos que da un total de 28, que es el número aproximado de días en un mes, y esto se repite también en las esquinas interiores.
Si multiplicamos el número 28 que obtuvimos sumando las esquinas, por el número 13, obtenemos el número 364. Si consideramos que los mayas empezaban a contar desde el cero, podemos ajustarlo esto a nuestro modo de contar, por lo que sumaremos un dígito al 364, lo que nos da 365, que es el número de días en un año solar.
El 20 y el 13 son las bases binarias del tzol'kin y se los eligen para establecer el inicio y fin de un código de ecuaciones antiguas. El 72 que mostraré en la siguiente secuencia descendente es curiosamente el ángulo de 72° en que luego del periodo sinódico de Venus de 583.92 días, el planeta aparece en una posición con respecto a la elongación anterior, tras ocho años que es precisamente la cantidad de dígitos binarios presentes en la secuencia que veremos, si bien la ecuación finalizada posee 9 valores al estar compuesta por dos partes. 7+2 es el 9 que es el fin de un sistema y a la vez lo infinito, mientras el 65 es el albedo de Venus, que es el porcentaje de radiación que su superficie refleja respecto a la radiación que incide sobre la misma, y multiplicado por 4 nos da la cantidad de días del tzol'kin, siendo el 4 solo un conector entre el mundo visible, que tiende a lo masculino al haber cambio en el mismo, con el mundo invisible y su realidad que es eterna y por ende sin cambio.
La ecuación:
01011000 = 0×20 + 1×19 + 0×18 + 1×17 + 1×16 + 0×15 + 0×14 + 0×13 = 52, que sumado a 13 nos da 65 y sumado a 20 nos da 72.
Dando vuelta la primer ecuación tenemos que:
10100111= 1×13 + 0×14 + 1×15 + 0×16 + 0×17 + 1×18 + 1×19 + 1×20= nos da 85, que restando 20 nos da 65 y restando 13 nos da 72.
Al dar vuelta la ecuación se nos permite apreciar que cada valor del 20 al 13 o del 13 al 20 guarda una relación binaria con conceptos astronómicos que a simple vista no son evidentes. La reducción de las cifras finales al ver el resultado al reducirlas a un solo dígito arroja conclusiones interesantes. En el caso del 65 da como resultado 2, y el 72 da 9. Pero mas importante es decir que el 65 es el origen del sistema y el 72 es el final. Además de originarse el 2 previamente se origina el 11 mediante la reducción del 65, por lo que se nos indica que el 65 es el origen del sistema, ya que el 11 refleja los dos polos creadores y por ende el origen de la creación. El 72, reducido a 9 indica el fin del sistema, ya que es el 3, el numero de la creación, multiplicado sobre si mismo, marcando por ende lo infinito y a su vez el fin. En ambos casos los resultados finales se obtienen sumando o restando los dos extremos de las ecuaciones, o sea el 13 y el 20. El 52, que es el valor que vemos como resultado en la primera parte de la primera ecuación, es la cantidad de años que tarda en repetirse el calendario maya, o sea 52 veces los 365 kines mayas, debido a la coincidencia de fechas entre el tzol'kin y el calendario solar maya tras ese tiempo, que es equivalente a 73 vueltas del tzol'kin.
Imágen: el calendario tzol'kin.
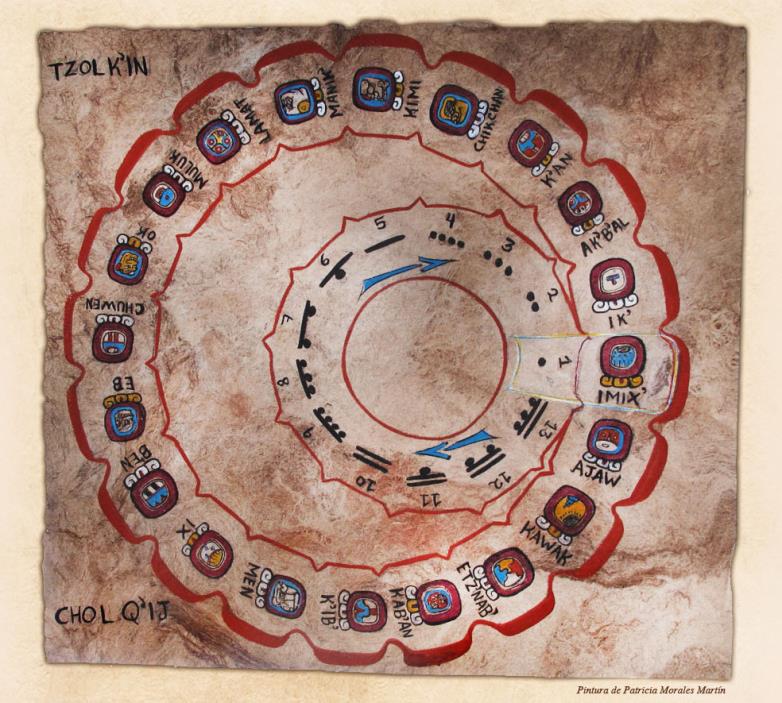
Un "Portador del Año" es el nombre de un día tzol'kin que ocurre en el primer día del Haabʼ, o sea el primer dia del calendario solar. Dado que hay 20 nombres para los días tzol'kin, 365 días en el calendario solar, y el resto de 365 dividido por 20 es 5 (365 = 18×20 + 5), el nombre de día tzol'kin para cada inicio del año solar será siempre el que este 5 puestos más adelante en el ciclo, en los 20 puestos que componen los nombres de los días tzol'kin. Como tal, la secuencia de fechas del tzol'kin correspondientes al primer día del calendario solar es la siguiente: 1 Ik' - 2 Manik' - 3 Eb' - 4 Kab'an - 5 Ik' ... 19 Eb' - 20 Kab'an - 1 Ik' ... Así, los Portadores del Año son los cuatro nombres de días tzol'kin que aparecen en esta secuencia: Ik', Manik', Eb' y Kab'an.
Por un lado, los cuatro años encabezados por los “Portadores del Año” llevan su nombre y comparten sus características; por lo tanto, también tienen sus propios pronósticos y deidades patronas. Además, dado que los Portadores del Año están identificados geográficamente con marcadores de límites o montañas, ayudan a definir la comunidad local. El sistema clásico de Portadores del Año descrito anteriormente se encuentra en Tikal y en el Códice de Dresde. Durante el Clásico Tardío se utilizó en Campeche un conjunto diferente de Portadores del Año. En este sistema, los Portadores del Año eran los tzol'kin que coincidían con el primer día del calendario solar. Estos fueron Ak'b'al, Lamat, B'en y Edznab.
Durante el Posclásico en Yucatán estuvo en uso un tercer sistema. En este sistema los Portadores del Año eran los días que coincidían con el segundo día del calendario solar: Kʼan, Muluc, Ix y Kawak. Este sistema se encuentra en la Crónica de Oxkutzcab. Además, justo antes de la conquista española, los mayas de Mayapán comenzaron a numerar los días del calendario solar también del 1 al 20. En este sistema los Portadores del Año son los mismos que en el sistema de Campeche. El sistema Clásico Portador del Año todavía está en uso en el altiplano guatemalteco y en Veracruz, Oaxaca y Chiapas, México.
Escrito exclusivamente para www.mundo24.info y www.mundo24.online
-------------------------------------------------------------
Diego Daniel García es graduado en antropología por la universidad estatal de Uruguay y ha publicado artículos en idioma ingles y serbio para el famoso portal ruso geopolitica.ru.
Durante toda una década, trabajó como escritor, publicando títulos en ingles (bajo el pseudonimo Pyotr Volkov). El largo recorrido expresado a través de sus dos obras: “Horizontes de la cuarta Teoría Política” (2019) y “Geopolitica del Apocalipsis” (2020)· abarca desde las religiones antiguas, el desarrollo de la ortodoxia cristiana y filósofos contemporáneos como el polémico pensador ruso Aleksandr Dugin.
Komentáře
Comentarios de Facebook
Los artículos más leídos por la última semana
- Empresas de "Israel" y Reino Unido saquearán petróleo de las Malvinas
- Georgescu: La OTAN iniciará la III Guerra Mundial desde Rumanía
- Argentina clama memoria, verdad, justicia y se levanta por Palestina
- Trump y Putin podrían traer la paz al mundo
- Presidente de Venezuela visitará Rusia en el Día de la Victoria
- Trump aplaza el diálogo con Putin hasta que se acepten las condiciones del alto el fuego
